数学(九上)- 第二十一章 一元二次方程
21.1 一元二次方程
- 3y2 – 5y = 7 – y, 像这样,等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程,叫做一元二次方程(quadratic equation in one unknown)。
- 一元二次方程的一般形式是: ax2 + bx + c = 0 (a不等于0)。
- 其中ax2是二次项,a是二次项系数;bx是一次项,b是一次项系数;c是常数项。
- 使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根(root)。
21.2 解一元二次方程
21.2.1 配方法
- 一般地,对于方程 x2 = p (I),
- (1) 当p > 0时,根据平方根的意义,方程(I)有两个不等的实数根
- x1 = -√P, x2 = √P
- (2) 当p = 0时,方程(I)有两个相等的实数根 x1 = x2 = 0;
- (3) 当p < 0时,因为对任意实数x,都有x2 >= 0,所以方程(I)无实数根。
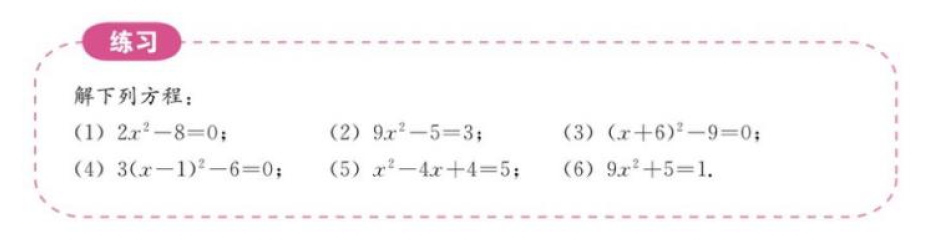
像上面那样,通过配成完全平方形式来解一元二次方程的方法叫做配方法。可以看出,配方是为了降次,把一个一元二次方程转化成两个一元一次方程来解。

21.2.2 公式法



21.2.2 因式分解法


21.2.2 一元二次方程的根与系数的关系

小结
一、本章知识结构图
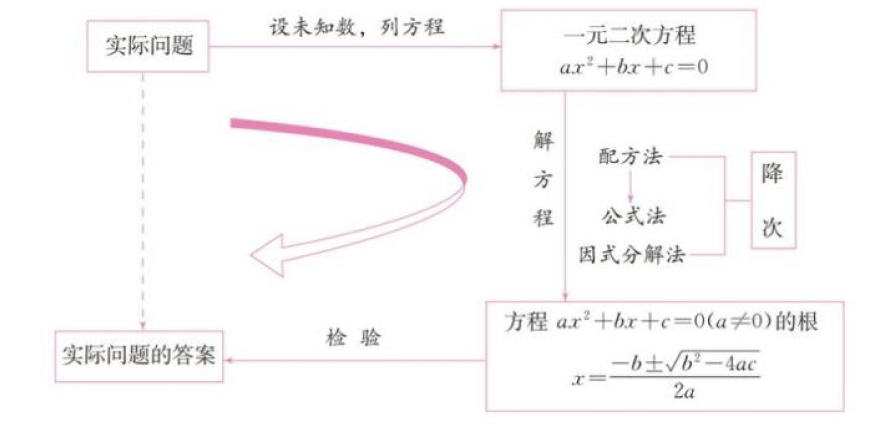
二、回顾与思考

